The Monty Hall Question: The shocking truth behind the mind game reveals a profound misunderstanding
summary：
In September 1990, Marilyn vos Savant answered a highly debated mathematical question in h... The Monty Hall Question: The shocking truth behind the mind game reveals a profound misunderstanding of human decision-making!
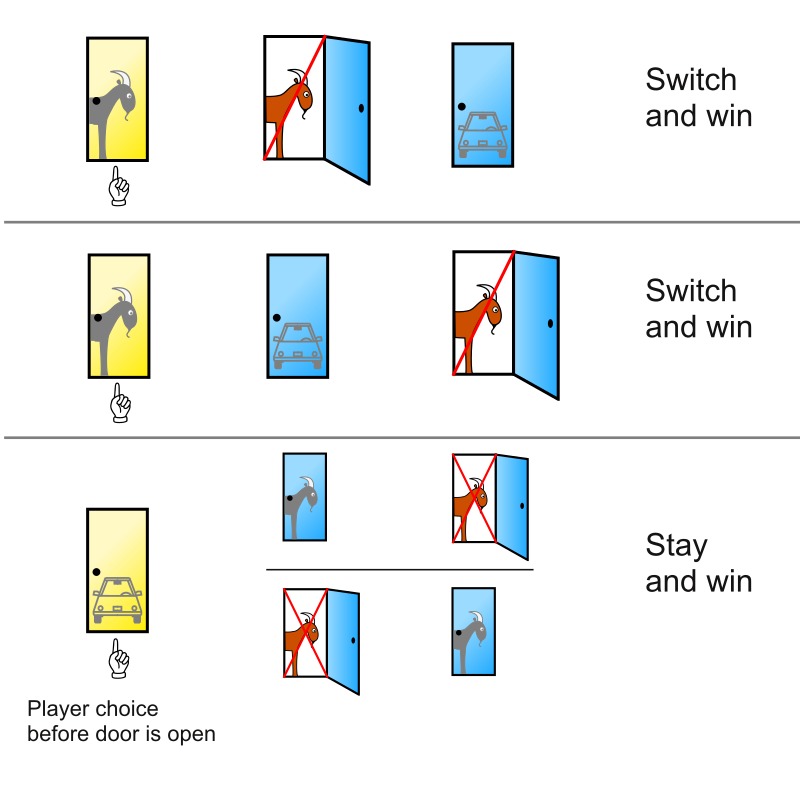
In September 1990, Marilyn vos Savant answered a highly debated mathematical question in her widely read column—the famous Monty Hall problem. Named after the American television game show host Monty Hall, this problem remains a classic case in probability theory. On the surface, the question seems simple: there are three doors, behind one of which there is a car, and behind the other two, there are goats. The contestant initially picks one door. The host then opens a different door to reveal a goat. The contestant is then given the option to either stick with their original choice or switch to another door. So, should the contestant switch doors to maximize their chances of winning the car? vos Savant’s answer was clear: “Yes, they should switch.” This conclusion sparked significant controversy, with many doubting her answer and even accusing her of being wrong, using phrases like “You completely messed up!”
However, vos Savant’s conclusion is correct. The underlying principles of probability are quite clear. Initially, the contestant’s probability of selecting the car is 1/3, while the probability of selecting a goat is 2/3. When the host opens a door with a goat, the car is now definitely behind one of the two remaining doors. If the contestant switches, their probability of winning the car increases to 2/3, whereas sticking with their original choice results in only a 1/3 chance. Computer simulations conducted at MIT and popular TV shows like MythBusters have confirmed this conclusion. Surprisingly, many of the scholars who initially opposed vos Savant later reanalyzed the problem and admitted they were wrong.
Why is this problem so counterintuitive? Most people mistakenly believe that after the host opens a door, the two remaining doors have equal probabilities of 50% each. This view overlooks the probability distribution formed by the initial choice. In fact, the probabilities from the initial selection remain unchanged despite the host revealing a goat. The key to the Monty Hall problem is that the host doesn’t randomly select a door to reveal a goat; rather, he always reveals a goat behind one of the two doors not initially chosen by the contestant. Therefore, switching doors results in a higher probability of winning.
vos Savant demonstrated remarkable mathematical talent in solving this problem. She not only scored exceptionally high on IQ tests (with a reported IQ of 228, surpassing many renowned figures like Einstein and Hawking), but her academic achievements are also noteworthy. From a young age, vos Savant exhibited extraordinary abilities, memorizing entire books by the age of 10 and reading through the Encyclopaedia Britannica. Despite her impressive intelligence, her path to success was not without obstacles. She had to withdraw from school due to family issues but later supported herself through self-study and writing. In 1985, vos Savant began contributing columns to Parade magazine, and with her response to the Monty Hall problem, she became a public figure.
Though vos Savant’s solution was initially mocked and dismissed, her eventual triumph not only demonstrated her intellectual capabilities but also highlighted the significant gap between intuition and logic when dealing with mathematical problems. The Monty Hall problem remains a classic example in probability theory, illustrating how people can easily fall prey to cognitive biases when confronted with seemingly simple questions. vos Savant’s answer sparked deeper discussions on probability, decision-making, and human cognition, reinforcing the value of sticking to the truth, even in the face of public skepticism.
Marilyn vos Savant stands as a symbol of intelligence and perseverance, inspiring everyone to remain steadfast in their beliefs and to pursue the correct answers, even when misunderstood or challenged.
Tags: Monty Hall problem, probability theory, intuition, IQ, mathematics
References:
